(GNN 記者 Edward 報導) 2018-04-04 00:30:23
隨著行動平台的發展以及硬體設備的提升,越來越多的手機遊戲如雨後春筍般冒出,讓人眼花撩亂,其中多數遊戲搭載了所謂「轉蛋」或是「抽卡」這樣的付費機制,讓玩家一窩蜂的投入大筆金錢,無非就是為了取得心愛的角色。
-

許多玩家常常為了喜愛的角色一擲千金
玩家們也各自擁有不同的抽卡/轉蛋信仰,有些人堅持單抽;某些玩家則是堅持十連抽才是王道,各式各樣的玄學讓玩家深信不已,即使沒有所謂的科學證據可以證明該方法真的有效,但透過玩家們之間的口耳相傳以及自身的經驗,仍讓這些不同的抽卡流派在玩家間佔有一席之地,今天筆者則是想透過一些簡單的觀點,來與大家分享關於「抽卡」這件事情。
「抽卡」玄學
儘管玩家們心知肚明抽卡這件事情只關乎「機率」而已,但碰到需要靠運氣來賭的時候,人往往會想藉助神佛的力量來扭轉乾坤,也因此發展出各式各樣的抽卡玄學,接下來筆者就為玩家簡單介紹一下常見的抽卡玄學。
單抽流派
如果在遊戲中沒有所謂「十連抽保底」,或是其他類似的獎勵機制時,許多玩家往往會選擇單抽。除了可以看比較多次轉蛋動畫之外,消耗虛擬貨幣的速度當然也是相對較慢的,讓玩家可以靜靜地欣賞轉蛋的過程。
更重要的是,單抽符合「雞蛋不要放在同一個籃子」的原則,避免讓辛苦累積的虛擬貨幣一瞬間消耗殆盡,卻什麼也抽到。當下空虛的心情,相信許多玩家都有深刻的體悟。
十連抽流派(連抽機制)
許多遊戲中常見的「十連抽」、「五連抽」等不同抽數的連抽機制,除了有些遊戲會提供類似「保底」機制外;也有的遊戲會給予額外獎勵或是多送一抽變成十一連抽、降低所需的虛擬貨幣等,藉此鼓勵玩家進行十連抽,包括《
怪物彈珠》、《
聖火降魔錄 英雄雲集》、《
超級鋼彈大亂戰》以及《
塗鴉大亂鬥》等遊戲都有類似的獎勵機制。
雖然客觀上來說十連抽與所謂單抽十次應該是一樣的機率,但如果常常透過十連抽抽出喜愛角色的玩家,就會對於十連抽有著比較好的印象,相信能延續這樣的好手感,選擇進行連抽。
特定時間抽流派
相信如果有遊玩《
Fate/Grand Order》的玩家或許有聽過,在日本曾有一位實況主在同一時間用不同裝置來抽卡,發現在同一時間中抽出相同卡的機率極高,也因此認為「時間」這項因素很有可能左右了抽卡的結果。讓許多玩家選擇在特定的時間進行抽卡,祈求能夠帶來好運。
有的玩家認為要在活動一開放時便搶先登入抽卡;有的玩家認為在整點 0 分 0 秒抽卡能帶來好運;部分玩家則是偏好清晨,而喜好半夜抽卡的玩家也不在少數,至於效果如何就見仁見智了。
無心流派
有的玩家認為,當你越想要抽到某張卡時,系統就越不會出現那張卡,因此許多玩家會戲稱「讀心晶片」正常運作中。為了避免這樣的情況,玩家往往會選擇讓朋友、家人,甚至是寵物來抽卡,希望借助他人的好運來一抽入魂。
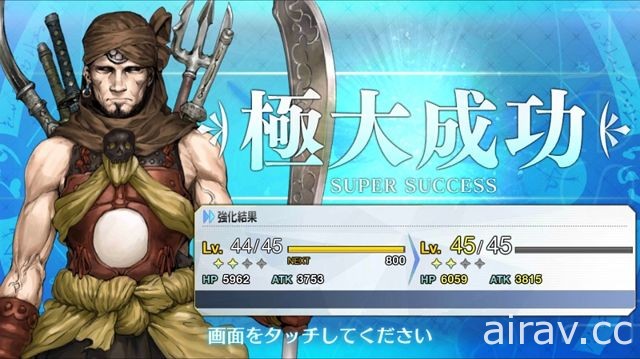
肥料強化大成功流派
大部分搭載抽卡、轉蛋機制的手機遊戲,都有導入培育角色這樣的系統,也因此玩家必須利用強化素材(俗稱肥料)來提升角色的等級或是技能、血量、攻擊力等素質。系統往往會導入所謂的強化成功、強化大成功等一定機率讓經驗獲取更加提升的隨機要素。
當玩家偶然在強化過程中碰到大成功時,往往會認為「現在的手氣不錯呢!」,也因此有些玩家選擇在強化碰到大成功或是超大成功等特效時,趕緊進入抽卡介面,看看能不能趕緊延續當下的好運。
友情抽卡流派
與上面提到的「肥料強化大成功流派」相同,只是本方法是透過遊戲中的「友情抽卡」,也就是僅需使用遊戲中的虛擬點數就能夠進行的抽卡來檢驗自身的運氣。如果抽出了友情卡池中的稀有角色,玩家就會認為目前的運氣不錯,可能是個抽卡的好時機。
從不同的科學理論來看「抽卡」這件事
何謂「賭徒謬誤」
賭徒謬誤(The Gambler's Fallacy)是一種機率謬誤,依據維基百科的解釋,主張由於某事發生了很多次,因此接下來不太可能發生;或者由於某事很久沒發生,因此接下來很可能會發生。
舉例來說,如果以賭徒謬誤來看擲硬幣這件事的話,連續出現越多次正面朝上,下次拋出正面的機率就越小,拋出反面的機率就越大。在 1913 年 8 月 18 日時,位於摩納哥的蒙地卡羅賭場,在賭輪盤的賭博中連續開出了 13 次黑色,因此現場的賭客們紛紛認為下一次一定會出現紅色,在紅色投下了高額賭注,然而第 14、15 次仍是黑色,賭客們繼續加碼,認為下一次就是紅色。
直到連續 26 次黑色之後,輪盤中才出現紅色,連續的黑色讓許多賭客血本無歸,賭場則是成了最大贏家。也因此賭徒謬誤(The Gambler's Fallacy),又被稱為蒙地卡羅謬誤(The Monte Carlo Fallacy)。
何謂「熱手謬誤」
熱手謬誤(The Hot Hand Fallacy )是一種機率謬誤,據維基百科定義,該理論主張由於某事件發生了很多次,因此下次再發生的機率很高。「熱手」這個名詞其實是源自於籃球這項運動,形容球員手感正好。舉例來說,假如 NBA 知名退役球星 Kobe Bryant 連續命中了好幾次投籃,那麼他下一次的出手命中率將會更高嗎?不少球迷可能會認為這是當然的,因為 Kobe Bryant 的手感正熱得發燙。
-

NBA 洛杉磯湖人隊退役球星柯比·布萊恩(Kobe Bryant)
不過事實真的是如此嗎?心理學家湯瑪斯·吉洛維奇(Thomas Gilovich)、羅伯特·瓦隆(Robert Vallone)以及認知心理學家阿摩司·特沃斯基(Amos Tversky)在 1985 年時提出統計數據證明,認為結論是「不會」。
他們使用 1980–82 賽季 NBA 波士頓塞爾提克隊(Boston Celtics)的罰球數據,分別就不同球員第 1 球罰進或是沒有罰進的情況下調查對於第 2 球的影響,數據顯示不論第 1 球有沒有進,都不影響第 2 球的命中率。
-

NBA 中的波士頓塞爾提克隊(Boston Celtics)以及費城七六人隊(Philadelphia 76ers)
另外也使用了 1980–81 賽季 NBA 費城七六人隊(Philadelphia 76ers)的數據進行分析,計算球員們分別在命中 1~3球,以及沒有命中 1~3 球後的下一次投籃命中率。研究者透過數據指出,如果「熱手效應」真的存在,那麼在連續投進 3 球後的下一次投籃命中率,應該要高於連續錯失 3 球後的下一次投籃,然而數據顯示,在這較為極端的兩種情況下, 第 4 球的命中率並無顯著差異。
值得一提的是,近年來隨著越來越多的數據統計方式公開,證據顯示出「熱手效應」並非不無可能,但人們很可能因為過於放大的感受而對於「熱手效應」有所誤解,同時在運動比賽中,運動員的身心狀態也許對於其表現有著更大的影響,因此究竟「熱手效應」是否存在,仍有待觀察。
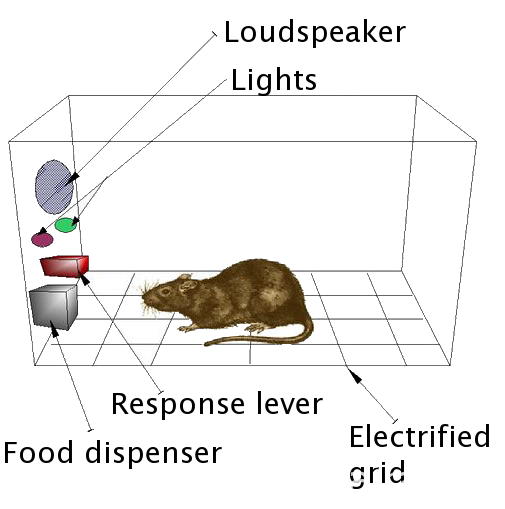
值得玩味的「史金納箱」實驗
美國心理學家伯爾赫斯·弗雷德里克·史金納(Burrhus Frederic Skinner)曾進行一項名為「史金納箱」(Skinner Box)的有趣實驗,史金納透過一個箱子連結操縱桿,而操縱桿與提供食物的機關相連,只要箱中的動物按壓操縱桿,該機關便會掉出食物至箱中。
史金納在箱中放置了飢餓的白鼠,而白鼠在箱中偶然碰觸到操縱桿,進而得到食物。白鼠經過多次嘗試,便開始不斷地按壓操縱桿,直到吃飽為止。透過這樣的條件性刺激讓動物有所反應;如果條件改為「不按操縱桿箱子就通電」,白鼠也會因此學會按壓操縱桿,不過只要箱子停止通電,白鼠的行為也立刻隨之消失,這代表儘管透過「懲罰」可以建立行為模式,不過效果十分短暫。
如果按下操縱桿,箱子會「機率性」的掉落食物,白鼠則是會不停地按下操縱桿,即便不斷降低機率,甚至是停止給予食物,白鼠的行為仍會持續很長一段時間。主要是由於白鼠即便沒有取得食物,也不會遭受到明顯的懲罰,因此仍會不斷進行嘗試,甚至很有可能導致行為的上癮。玩家花費金錢,機率性的取得虛擬道具或寶物,和此行為則有些類似。
有趣的是,如果白鼠在掉落食物前,偶然在從事一些無意義的行為,例如旋轉、撞擊箱子,白鼠便會培養出這樣奇異的行為習慣,認為透過這些行為就能取得食物,事實上這些行為無非與人類的「迷信」十分相似。
透過上述理論來分析「抽卡」
那麼如果是抽卡呢?玩家在抽到稀有度高的角色時,往往會認為現在運氣正好,繼續抽下去應該很有可能繼續抽出稀有的角色。人們會將每次隨機抽取之間獨立的機率建立不經意地建立關係,忽略了理性的機率統計。除非遊戲中有特殊的機率設定,不然每一次的抽取機率並不會因為前一次的抽取結果而有所影響。
以遊戲中的轉蛋為例,有些玩家會認為,此次幸運轉出 SSR 角色,接下來連續轉出 SSR 角色的機率將會較低,因此選擇先不轉蛋;或是相反的,由於一直沒有轉出 SSR 角色,因此認為接下來轉出 SSR 角色的機率將會有所提升,這兩種狀況下都是落入了賭徒謬誤的圈套。
事實上,每一次的轉蛋及抽卡都是所謂的「獨立事件」,而非「連續事件」,並不會因為前次或是連續出現的結果改變下次的結果。對此,以色列心理學學者阿摩司·特沃斯基(Amos Nathan Tversky)以及丹尼爾·康納曼(Daniel Kahneman)則提出了所謂的「小數法則」這樣的結論。當在不確定的情況下,人類的思考方式會系統性的選擇走向捷徑而偏離理性。
舉例來說,擲硬幣正反面各為 50% 的情況下,並不代表投擲 10 次會出現 5 次正面 5 次反面,即便投擲 10000 次的情況下也不一定會出現 5000 次正面及 5000 次反面。從數學的觀點來看,只能肯定當擲硬幣的次數越多時,正面及反面的比例會更趨近於 1:1。假設抽出 SSR 角色的機率為 1%,這並不代表每 100 次抽卡中會獲得 1 隻 SSR 角色,只能說抽卡次數越多時,抽出 SSR 角色的機率就會越趨近於 1%。
多數人面對不確定機率事件發生時,往往會不自覺地違反「大數法則」選擇走向「小數法則」,學者認為,由於人們對於環境中的機率推論通常是倚賴某種經驗或是頓悟,導致往往會做出偏差判斷。大家都知道擲硬幣出現正反面的機率在公平的情況下皆為 50%,但在連續擲出 5 個正面之後,多數人就傾向於判斷下一次出現反面的機率較大。這樣的預測錯誤便是將大樣本中的結論誤植到小樣本下的結果。
所以玩家如果在喜愛的遊戲中花錢抽卡轉蛋,仍應理性的判斷自身經濟實力以及抽中角色的機率,避免猶如史金納實驗中的白鼠行為成癮,過度沉迷卻不自覺。儘管不能真正確定究竟上述所提到的「抽卡玄學」是否有效,但不論是使用怎麼樣的玄學來抽卡、轉蛋,玩家都不宜過度迷信,或是過度依賴自身及他人的經驗來作為判斷基準,畢竟唯有冷冰冰的機率才是最真實的。